[Python][フィボナッチ数]Python3でフィボナッチ数を高速に求める方法

Table of Contents

フィボナッチ数

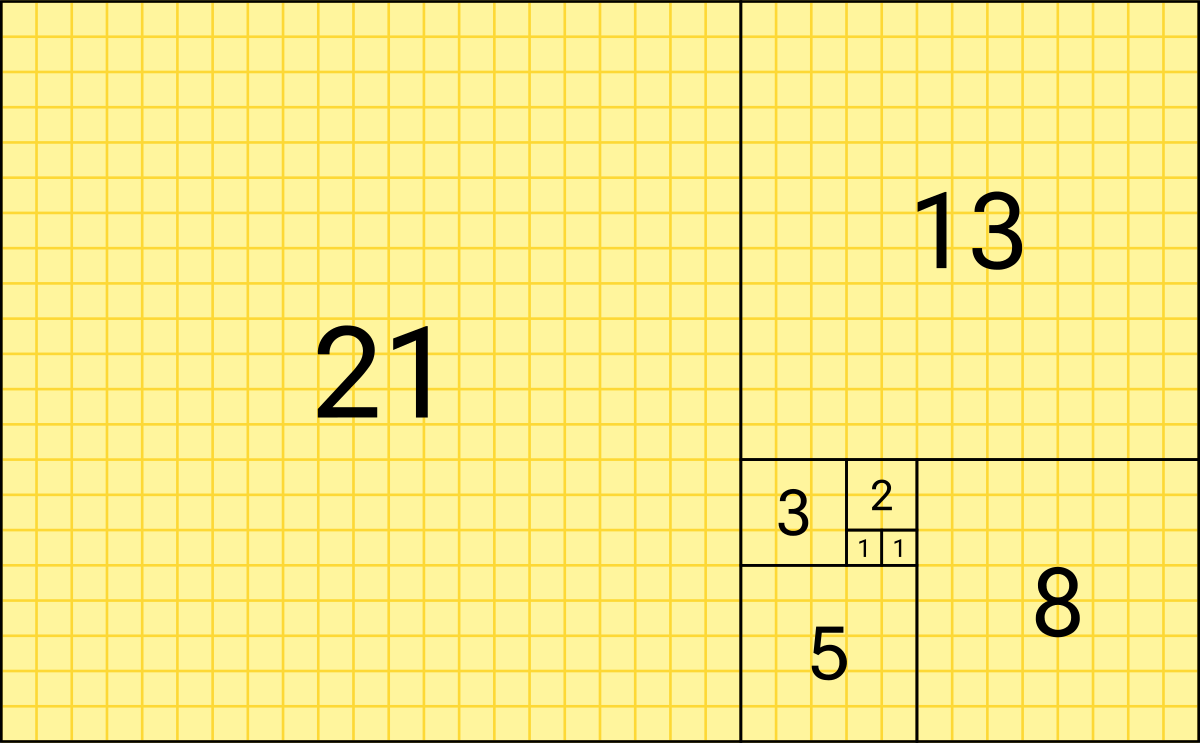
フィボナッチ数は$$F_{n+2} = F_{n+1} + F_{n}, F_1 = F_2 =1$$で定義される。

Pythonでフィボナッチ数を求める方法

普通にやろうとすると、再帰を用いて以下のようになるが、極めて遅い。なお、indexが上の定義とひとつずれていることに注意。

def fib(n):
    if n <= 1:
        return 1
    else:
        return fib(n-2) + fib(n-1)

$n = 100$ですら計算が全く終わらない。以下のようにchache化することで速度は向上する(0.008sec)。

import sys
sys.setrecursionlimit(10**6)
from functools import lru_cache
@lru_cache(maxsize = None)
def fib(n):
    if n <= 1:
        return 1
    else:
        return fib(n-2) + fib(n-1)
fib(100)
# 573147844013817084101

$n = 10,000$程度ならすぐに求めることができる。

メモ化

上記は再帰を用いているので遅いが、メモ化することで何回も同じ計算を繰り返さなくても良くなる。

import sys
sys.setrecursionlimit(10**6)
limit = 4000000

fib_memo = [0] * limit
def fib(n):
    if n <= 2:
        return n
    elif fib_memo[n] != 0:
        return fib_memo[n]
    else:
        fib_memo[n] = fib(n-1) + fib(n-2)
        return fib_memo[n]

$n = 10,000$のとき0.078sec程度で計算できる。ただし、$10$万以上になると計算が終わらないか、あるいはエラーとなる。

その他の方法

以下が簡単な割には早い。

sys.setrecursionlimit(10**6)
def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    a, b = 0, 1
    for _ in range(n - 1):
        a, b = b, a + b
    return b

fib(10000)

$n = 10,000$で$0.014$sec程度。ただし、$n = 100,000$ではエラーになる。

行列計算を利用

フィボナッチ数を計算するとき、行列を利用する方法もある。$$\begin{pmatrix}F_{n+1} & F_n \\ F_n & F_{n-1}\end{pmatrix} = \begin{pmatrix}1 & 1 \\ 1 & 0\end{pmatrix}^n$$となることを利用する。高速であるが、indexに注意する。

from itertools import product
def mat2_mul(X, Y):
    Z = [[0, 0],
         [0, 0]]
    for (i, j, k) in product(range(2), range(2), range(2)):
        Z[i][j] += X[i][k] * Y[k][j]
    return Z

def mat2_pow(X, n):
    if n == 0:
        return [[1, 0],
                [0, 1]]
    elif n % 2:
        return mat2_mul(X, mat2_pow(X, n-1))
    else:
        half_pow = mat2_pow(X, n/2)
        return mat2_mul(half_pow, half_pow)

def fib(n):
    if n == 0:
        return 0
    else:
        F = [[0, 1],
             [1, 1]]
        return mat2_pow(F, n-1)[1][1]

$n = 10,000$で$0.004$secと早いが、やはり大きい$n$には対応できない。

フィボナッチ数の先頭の数字

フィボナッチ数は一般項が$\displaystyle F_n = \frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)$で表されるので、$n$が大きいとき$\displaystyle F_n \approx \frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n$で近似できる（$\displaystyle \left|\frac{1-\sqrt{5}}{2}\right| < 1$であるから）。対数を取ると、$$\log{F_n} \approx n\cdot \log{\left(\frac{1+\sqrt{5}}{2}\right)}-\log{\sqrt{5}}$$となる。$\log{F_n}$は実数で、整数を$n$、小数部分を$t$とすると、$\log{F_n} = n + t\ (0\leq t<1)$となる。つまり、$F_n = 10^{t}\times 10^{n}$となるので、$10^t$についての情報が$F_n$の先頭についての情報になる。例えば、$F_n$の先頭$5$桁の数字が知りたければ、

from math import log10, sqrt
a = n * log10((1+sqrt(5))/2)-log10(sqrt(5))
a = int((pow(10, a - int(a) + 4)))

とすれば、$a$が$F_n$の先頭$5$桁を表すこととなる。同様に先頭$k$桁が知りたければ、

from math import log10, sqrt
a = n * log10((1+sqrt(5))/2)-log10(sqrt(5))
a = int((pow(10, a - int(a) + k-1)))

とすると良い。

フィボナッチ数(Fibonacci number)の全てフィボナッチ数列についてのまとめ