 math
math [math][京都大学]2024年京都大学理系数学問題5
問題
\(a\)は\(a\geq 1\)を満たす定数とする。座標平面上で、次の\(4\)つの不等式が表す領域を\(D_a\)とする。$$x\geq0,\ \frac{e^{x}-e^{-x}}{2}\leq y,\ y\leq \f...
 math
math  math
math  math
math  math
math  math
math  math
math  math
math  math
math 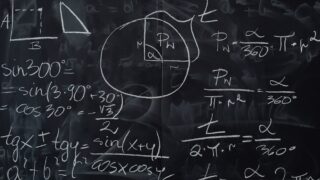 math
math  math
math