 math
math [math][東京医科歯科大学][微分]2002年東京医科歯科大学数学問題3
問題
正の整数\(n\)に対し、関数\(f_n(x)\)を次式で定義する。$$f_n(x) = \int_{1}^{x}{(x-t)^ne^{t}dt}$$(\(e\)は自然対数の底)。このとき以下の各問いに答えよ。\((1)\) ...
 math
math  math
math  math
math  math
math 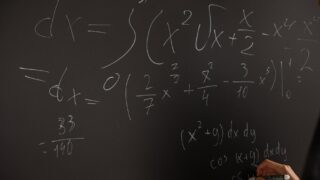 math
math  math
math  math
math  math
math  math
math  math
math