 math
math [math]2013年東京医科歯科大学数学問題3
問題
\(m, n\)を自然数として、関数\(f(x) = x^m(1-x)^n\)を考える。このとき以下の各問いに答えよ。\((1)\) \(0\leq x\leq 1\)における\(f(x)\)の最大値を\(m, n\)を用いて...
 math
math  math
math  math
math  math
math 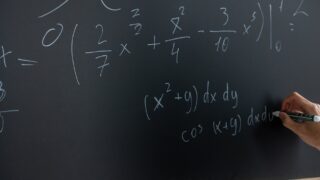 math
math  math
math  math
math  math
math  math
math  math
math