 math
math [math][東京科学大学]2025年東京科学大学(旧東京工業大学)数学問題1
問題
関数\(f(x)\)を\(x\geq 0\)に対して\(f(x) = x\log{(1+x)}\)と定める。\((1)\) 不定積分\(\displaystyle \int{x\log{(1+x)}dx}\)を求めよ。\((2...
 math
math  math
math  math
math  math
math 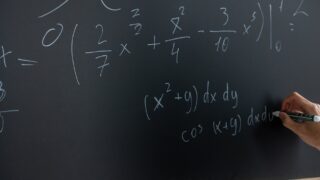 math
math  math
math